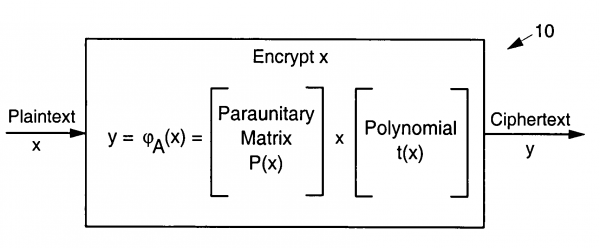
Georgia Tech inventors have created multivariate paraunitary asymmetric cryptographic systems and methods based on paraunitary matrices. The cryptographic systems and methods are based on formulating a system of multivariate polynomial equations by paraunitary matrices. These matrices are a family of invertible polynomial matrices that can be completely parameterized and efficiently generated by primitive building blocks. Using a general formulation involving paraunitary matrices, a one-way function is designed that operates over the fields of characteristic two. Approximations made to a paraunitary matrix result in a trapdoor one-way function that is efficient to evaluate, but hard to invert without secret information about the trapdoor.
- Short key size
- Short key-setup time
- Low complexity
- Fast encryption and decryption
- Maintained security
- Flexible design
- Exchanging keys
- Digital signatures
- Data authentication schemes
The principal of public-key cryptography involves exchanging information between parties without requiring a secure channel. In a public-key system, each party has a pair of secret and public keys. Everyone can send encrypted messages to a designated party using its public key. However, only the designated party can decrypt using his corresponding secret key. Public-key systems are used for the exchange or the distribution of secret keys that are used in symmetric cryptosystems. A well-known public-key cryptosystem, RSA, uses a univariate monomial over a very large ring. Although RSA has not been broken yet, there are some practical problems in its implementation. The first problem is the key-setup time is too long for computationally-limited processors used in some applications such as pervasive computing. A second problem is the size of the key, which is too long in applications where bandwidth is limited.